Комбинаторика
Сочетания
Сочетаниями из n элементов по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые различаются хотя бы одним элементом ( в сочетаниях не учитывается порядок элементов).
Из четырех фруктов: груша, яблоко, лимон, апельсин создать группы по два фрукта.
Количество групп равно 6.
Формула для нахождения количества сочетаний из n элементов по m:
Из четырех фруктов: груша, яблоко, лимон, апельсин создать группы по два фрукта.
Формула для нахождения количества сочетаний из n элементов по m:
Пример: Возьмем буквы Б, А, Р. Какие сочетания из этих букв, взятых по две, можно получить? Сколько таких наборов получится, если буквы в наборе не повторяются?
Получатся наборы: БА (БА и АБ - один и тот же набор), АР и РБ.
Сочетания с повторениями
Из n элементов, взятых по m, где элементы в наборе могут повторяться.
Из четырех фруктов: груша, яблоко, лимон, апельсин создать группы по два фрукта, но можно брать по два одинаковых фрукта.
Из четырех фруктов: груша, яблоко, лимон, апельсин создать группы по два фрукта, но можно брать по два одинаковых фрукта.
Количество групп равно 10.
Формула для нахождения количества сочетаний с повторениями из n элементов по m:
Пример: Возьмем буквы Б, А, Р. Какие сочетания из этих букв, взятых по две, можно получить? Сколько таких наборов получится, если можно брать по две одинаковые буквы.
Получатся наборы: ББ, БА, БР, АА, АР, РР.
Размещения
Размещениями из n элементов по m элементов (m < n) называются комбинации, составленные из данных n элементов по m элементов, которые отличаются либо самими элементами, либо порядком элементов.
Составить всевозможные группы из трех фруктов: груша, яблоко, лимон по два фрукта, порядок следования элементов учитывается.
Количество групп равно 6.
Формула для нахождения количества размещений из n элементов по m:
Составить всевозможные группы из трех фруктов: груша, яблоко, лимон по два фрукта, порядок следования элементов учитывается.
Формула для нахождения количества размещений из n элементов по m:
Пример: Возьмем буквы Б, А, Р. Какие размещения из этих букв, взятых по две, можно получить? Сколько таких наборов получиться, если буквы в наборе не повторяются?
Получатся следующие наборы: БА, БР, АР, АБ, РБ, РА.
Размещения с повторениями
Размещениями с повторениями из n элементов по m называются упорядоченные m-элементные выборки, в которых элементы могут повторяться.
Количество групп равно 9.
Формула для нахождения количества размещений с повторениями из n элементов по m:
Пример. Всевозможные размещения с повторениями из трех элементов a, b, c по 2:
ab, ac, bc, aa, bb, cc, ba, ca, cb
Перестановки
Перестановками из n элементов называются размещения из этих n элементов по n (Перестановки - частный случай размещений).
Переставить три фрукта: яблоко, груша, лимон различными способами.
Количество перестановок равно 3.
Формула для нахождения количества перестановок из n элементов:
Переставить три фрукта: яблоко, груша, лимон различными способами.
Формула для нахождения количества перестановок из n элементов:
Пример: Возьмем буквы Б, А, Р. Какие перестановки из этих букв можно получить? Сколько таких наборов получится, если буквы в наборе не повторяются?
Получатся наборы: БАР, БРА, АРБ, АБР, РАБ, РБА.
Перестановки с повторениями
k различных элементов, где элементы могут повторяться m1, m2, …, mk раз и m1 + m2 +… + mk = n, где n - общее количество элементов).
Создать всевозможные перестановки из одной груши и трех яблок.
Количество перестановок равно 4.
Формула для нахождения количества перестановок с повторениями из k различных элементов, где элементы могут повторяться m1, m2, …, mk раз и m1 + m2 +… + mk = n, где n - общее количество элементов):
Создать всевозможные перестановки из одной груши и трех яблок.
Формула для нахождения количества перестановок с повторениями из k различных элементов, где элементы могут повторяться m1, m2, …, mk раз и m1 + m2 +… + mk = n, где n - общее количество элементов):
Пример: Возьмем буквы Б, А, Р. Какие перестановки из этих букв можно получить? Сколько таких наборов получится, если буква А повторяется два раза?
Получатся наборы: БАРА, БРАА, БААР, ААРБ, ААБР, АБАР, АРАБ, АРБА, АБРА, РАБА, РААБ, РБАА.
Задачи
1. Сколькими способами можно вывезти со склада 10 ящиков на двух автомашинах, если на каждую автомашину грузят по 5 ящиков?
Посмотреть решение
Посмотреть решение
2. В почтовом отделении продаются открытки 10 видов. Сколькими способами можно купить 12 открыток для поздравлений?
Посмотреть решение
Посмотреть решение
3. Расписание одного дня состоит из 5 уроков. Определить число вариантов расписания при выборе из 11 дисциплин.
Посмотреть решение
Посмотреть решение
4. Шифр сейфа состоит только из 6 цифр, которые должны набираться последовательно и могут повторяться. Чему в этом случае равно общее число всех возможных комбинаций шифра?
Посмотреть решение
Посмотреть решение
6. Сколькими способами можно расставить белые фигуры (короля, ферзя, 2 ладьи, 2 слонов и 2 коней) на первой линии шахматной доски?
Посмотреть решение
7. Сколькими способами из колоды в 36 карт можно выбрать 3 карты?
Посмотреть решение
Посмотреть решение
7. Сколькими способами из колоды в 36 карт можно выбрать 3 карты?
Посмотреть решение
8. В классе 23 человека. Сколькими способами можно выбрать старосту и его заместителя?
Посмотреть решение
Посмотреть решение
10. В кошельке находится достаточно большое количество рублей, 2-х, 5-ти и десятирублёвых монет. Сколькими способами можно извлечь три монеты из кошелька?
Посмотреть решение
Знак «плюс» следует понимать и читать как союз ИЛИ.
Пример: Класс состоит из 23 человек, среди которых 10 мальчиков и 13 девочек. Сколькими способами можно выбрать 2-х человек одного пола?
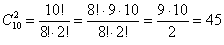способами можно выбрать 2-х мальчиков;
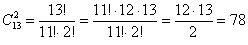способами можно выбрать 2-х девочек.
Задача. Имеем а фруктов и b конфет. Сколько подарков по n фруктов и k конфет можно сформировать?
2. При встрече каждый из друзей пожал другому руку. Сколько всего было рукопожатий, если встретились 6 друзей?
3. Сколько существует вариантов рассаживания вокруг стола 6 гостей на 6 стульях?
9. Предприятие может предоставить работу по одной специальности 4 женщинами, по другой - 6 мужчинам, по третьей - 3 работникам независимо от пола. Сколькими способами можно заполнить вакантные места, если имеются 14 претендентов: 6 женщин и 8 мужчин?
Посмотреть решение
Сложение
Знак «плюс» следует понимать и читать как союз ИЛИ.Пример: Класс состоит из 23 человек, среди которых 10 мальчиков и 13 девочек. Сколькими способами можно выбрать 2-х человек одного пола?
В данном случае не годится подсчёт количества сочетаний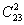 
, поскольку множество комбинаций из 2-х человек включает в себя и разнополые пары.
Условие «выбрать 2-х человек одного пола» подразумевает, что необходимо выбрать двух мальчиков или двух девочек:
, поскольку множество комбинаций из 2-х человек включает в себя и разнополые пары.Условие «выбрать 2-х человек одного пола» подразумевает, что необходимо выбрать двух мальчиков или двух девочек:
способами можно выбрать 2-х мальчиков; способами можно выбрать 2-х девочек.
Таким образом, двух человек одного пола можно выбрать: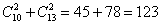 
способами.
Ответ: 123. способами.Умножение
Знак «умножить» следует понимать и читать как союз И.
Пример: Сколько существует трёхзначных чисел, которые делятся на 5?
Обозначим данное число тремя звёздочками: ***
Комбинации будем считать по разрядам – слева направо:
В разряд сотен можно записать любую из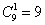
цифр (1, 2, 3, 4, 5, 6, 7, 8 или 9). Ноль не годится, так как в этом случае число перестаёт быть трёхзначным.
В разряд десятков («посерединке») можно выбрать любую из 10-ти цифр: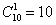
.
Обозначим данное число тремя звёздочками: ***
Комбинации будем считать по разрядам – слева направо:
В разряд сотен можно записать любую из
цифр (1, 2, 3, 4, 5, 6, 7, 8 или 9). Ноль не годится, так как в этом случае число перестаёт быть трёхзначным.В разряд десятков («посерединке») можно выбрать любую из 10-ти цифр:
.
По условию, число должно делиться на 5. Число делится на 5, если оно заканчивается на 5 либо на 0. Таким образом, в младшем разряде нас устраивают 2 цифры.
Итого, существует: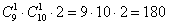
трёхзначных чисел, которые делятся на 5.Ответ: 180.
Итого, существует:
трёхзначных чисел, которые делятся на 5.Ответ: 180.Задача. Имеем а фруктов и b конфет. Сколько подарков по n фруктов и k конфет можно сформировать?
Экспериментальный раздел
1. При окончании деловой встречи специалисты обменялись визитными карточками. Сколько всего визитных карточек перешло из рук в руки, если во встрече участвовали 6 специалистов?2. При встрече каждый из друзей пожал другому руку. Сколько всего было рукопожатий, если встретились 6 друзей?
3. Сколько существует вариантов рассаживания вокруг стола 6 гостей на 6 стульях?
4. Сколькими способами 10 футбольных команд могут разыграть между собой золотые, бронзовые и серебряные медали?
5. В меню столовой предложено на выбор 2 первых блюда, 6 вторых и 4 третьих блюда. Сколько различных вариантов обеда, состоящего из первого, второго и третьего блюда, можно составить?
6. Секретный замок состоит из 4 барабанов, на каждом из которых можно выбрать цифры от 0 до 9. Сколько различных вариантов выбора шифра существует?
7. Сколько различных трёхзначных чисел можно составить при помощи цифр 4, 7, 9? (Цифры в записи числа не повторяются).
Сколько различных трёхзначных чисел можно составить с помощью цифр 1, 3, 7? (Цифры могут повторяться).
7. Сколько различных трёхзначных чисел можно составить при помощи цифр 4, 7, 9? (Цифры в записи числа не повторяются).
Сколько различных трёхзначных чисел можно составить с помощью цифр 1, 3, 7? (Цифры могут повторяться).
8. Сколько нечетных трёхзначных чисел можно составить из цифр 3, 4, 8, 6? (Цифры в записи числа не могут повторяться).
9. Предприятие может предоставить работу по одной специальности 4 женщинами, по другой - 6 мужчинам, по третьей - 3 работникам независимо от пола. Сколькими способами можно заполнить вакантные места, если имеются 14 претендентов: 6 женщин и 8 мужчин?
10. Для участия в команде тренер отбирает 5 мальчиков из 10. Сколькими способами он может сформировать команду, если 2 определенных мальчика должны войти в команду?
Задания для самостоятельного решения
1. Сколькими способами можно отобрать 12 книг из 20 и расставить их в ряд на полке?
2. Переплетчик должен переплести 14 различных книг в красный, зеленый и коричневые переплеты. Сколькими способами он может это сделать?
3. Сколькими способами 4 юноши могут пригласить четырех из шести девушек на танец?
4. У одного человека 7 книг по математике, а у второго – 9. Сколькими способами они могут обменять друг у друга две книги на две книги.
5. В кондитерском магазине продавались 4 сорта пирожных: эклеры, песочные, наполеоны и слоеные. Сколькими способами можно купить 7 пирожных.
6. Сколькими способами можно выбрать гласную и согласную буквы из слова «здание»?
7. Дано n различных бусин. Сколько различных ожерелий можно составить из них?
